This is a small post on how to try to get realistic four-dimensional spacetimes from type IIA and type IIB string theories. I will try to explain the technical points as much as I can. I will assume the knowledge of metric, Ricci, and Riemann tensors and very basic QFT. Let me know if some point needs clarification.

Type IIA and type IIB string theories both live in 10-dimensional spacetime and one approach to bring them to 4-dimensional spacetime is to compactify the rest of 6 space dimensions. Ok but what kind of compact 6-dimensional space is made by these 6 dimensions? The answer to this question depends on what we want to have.

The 10D spacetime has a metric tensor and when this spacetime is divided into a compact 6D space (let’s call this space Y) and a noncompact 4D spacetime (let’s call this spacetime X), the metric tensor also divides into two parts (i.e. one part for X and one for Y). However, is X’s metric independent of the coordinates of Y? Well, not necessarily. We elaborate on this point now.
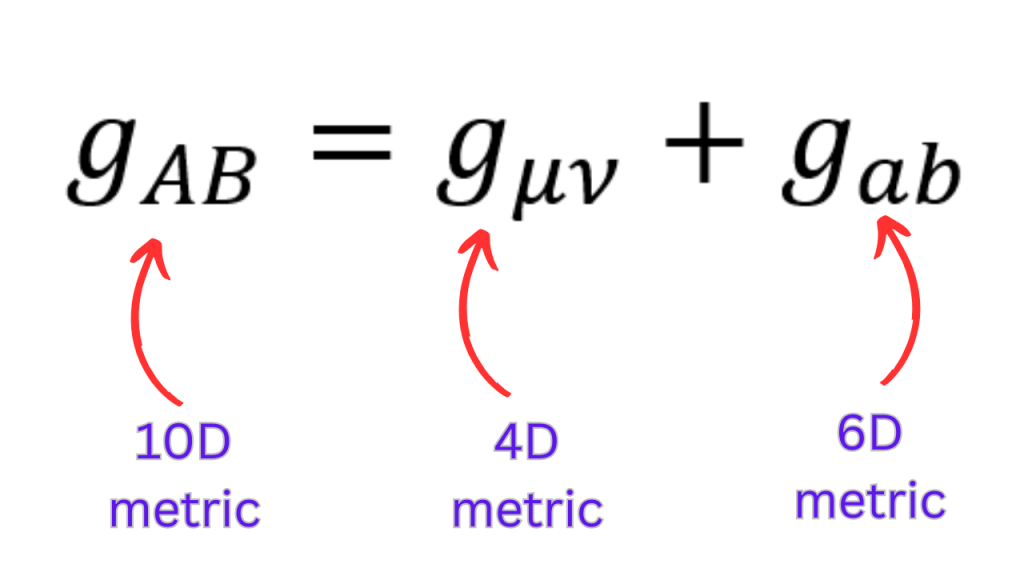
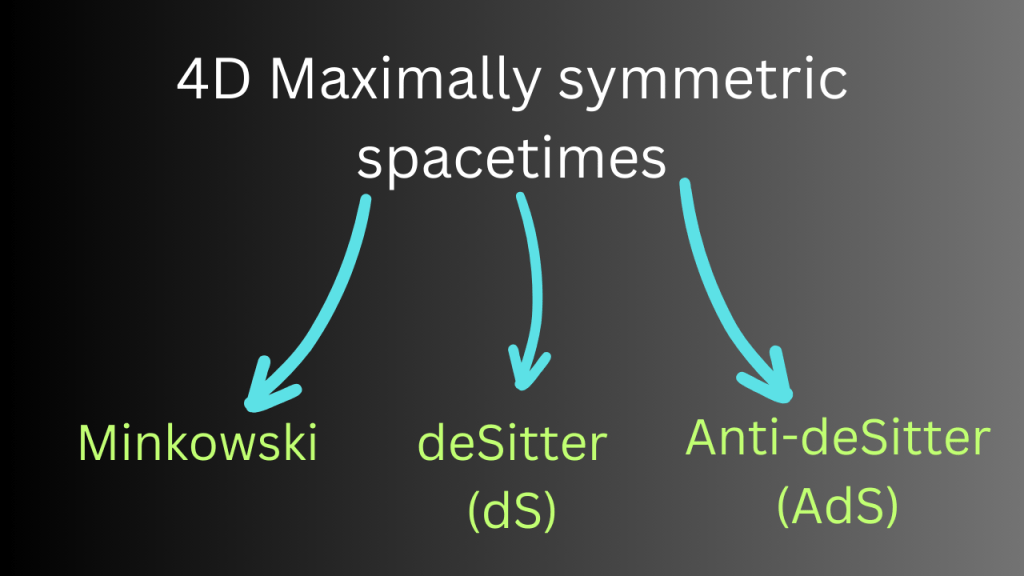
We can require that X is a ‘maximally symmetric’ spacetime which means that it has the maximum symmetry that a 4D spacetime can have. The well-known Minkowski spacetime is maximally symmetric but it is not the only one. Apart from Minkowski spacetime, we also have deSitter spacetime (also called dS) and Anti-deSitter spacetime (also called AdS). deSitter and Anti-deSitter spacetimes have constant positive and negative curvatures respectively.
Now, if X is maximally symmetric and we multiply X’s metric with a positive function which is dependent on Y’s coordinates, it turns out that the resulting metric for X is still maximally symmetric. So, generally, X’s metric can be dependent on Y’s coordinates but in the sense described above. This function is called the warp factor. Let’s call this factor A.
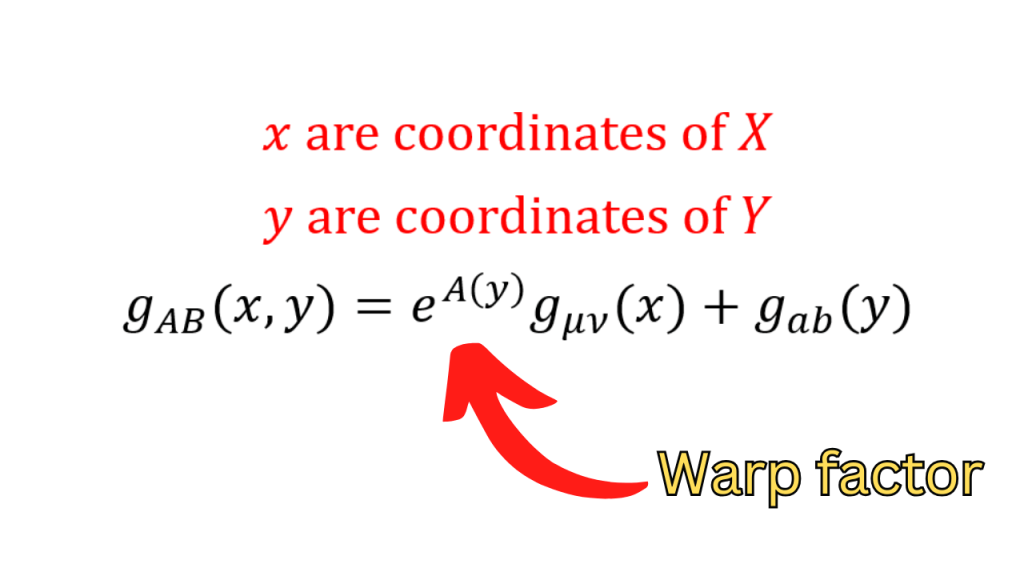
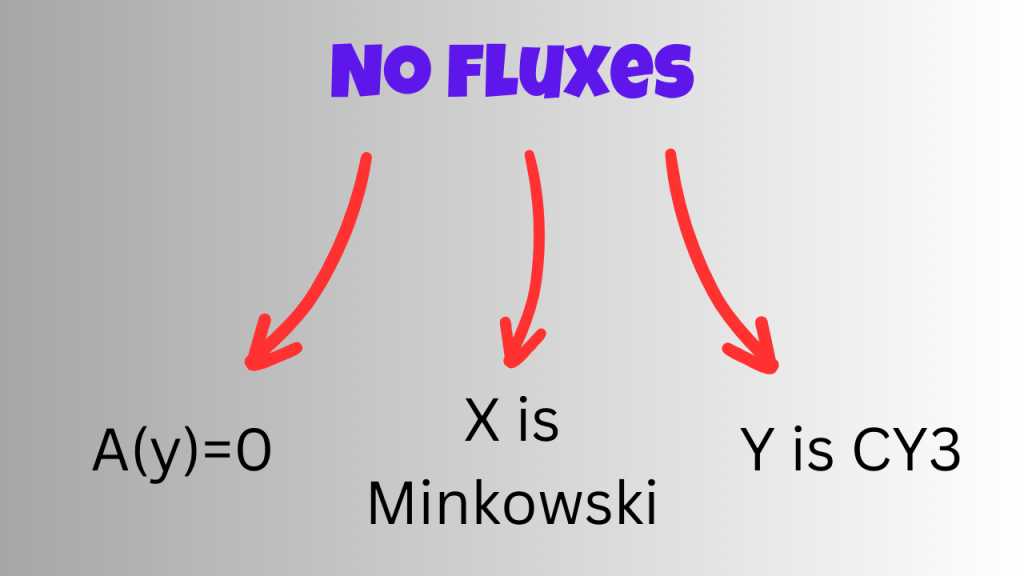
Now, type II string theories contain gravitons, fermionic fields and, other fields called fluxes. In the first case, we exclude the fluxes (referred to as ‘turn off the fluxes’). Turning off the fluxes implies that the fermion fields in type II theories should be ‘covariantly constant’ i.e. their covariant derivative vanishes. This condition in turn implies that A has to be zero and that X has to be a Minkowski space. It also implies that Y has to be a special space called Calabi-Yau 3 fold (called CY3).
So what’s the problem with this construction? Firstly, we didn’t turn off the fluxes and thus, it is an interesting problem to see what will happen if we do so. The big problem is that X is Minkowski while we know that our 4D spacetime is dS. Moreover, we have N=2 supersymmetry in X and it is a problem because it doesn’t allow for chiral fermions (i.e. left and right-handed fermions behave similarly) which shouldn’t be the case because parity is violated in our universe.
Let’s focus on the first problem. Let’s try to make X a dS spacetime. There is a no-go theorem due to Maldacena and Nunez (it uses Einstein field equations) which says that even if you use fluxes, you can’t get dS but only Minkowski or AdS spacetime. Is this a disaster? No, it is not because we can add localized charges into our theory as well. The localized charges for string theory are carried by D branes.
D branes are extended objects. A particle has zero spatial dimensions, a string has one spatial dimension, and so on. A D-brane with p spatial dimensions is called a Dp-brane. It turns out that if we use Dp-branes with p<7, then we still can’t get 4D dS spacetime. One important point is that all these no-go theorems aren’t derived using supersymmetry. So they are valid whether or not supersymmetry is there.
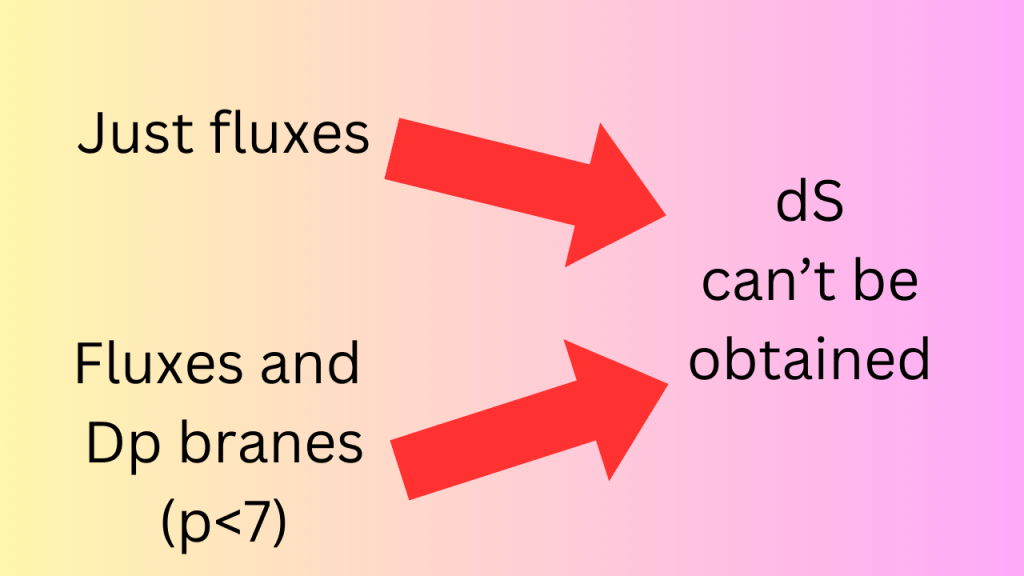
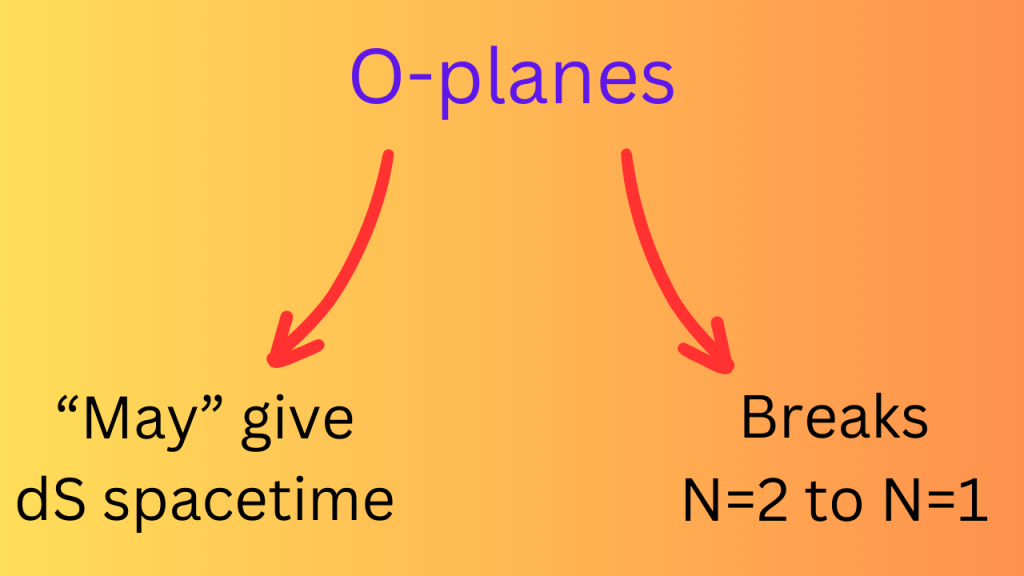
To counter this puzzle, we put some more objects into our theory called the orientifold planes (also called the O planes). O planes are extended objects like D branes except that they have ‘negative tension’ while D branes have ‘positive tension’. It also turns out that we can’t just choose the number of D branes and O planes to put in our theory. This is the case because there are some conditions on their numbers that have to be satisfied.
These conditions are called tadpole cancellation conditions and they are derived by equations of motion of fluxes and the constraints that these fluxes satisfy. These constraints are called the Bianchi identities of the fluxes. Bianchi identities are also found in ordinary electrodynamics and thus, they should be familiar to the reader. Tadplole cancellation conditions relate the number of D branes to the number of O planes that you can have in your theory.

Adding O planes at least revokes the impossibility of getting dS spacetime but still, well-behaved dS constructions are rarely known (some would argue that there are no well-behaved dS constructions).
Let’s come to the second problem that we were having before i.e. how to get N=1 supersymmetry instead of N=2. It turns out that even this problem is solved by O planes. O planes break the N=2 supersymmetry to N=1 supersymmetry. So, we can kill two birds with one stone.
Now, another problem that faces us is that when we do all of these compactifications, we get a lot of extra particles in our theory. These particles are called moduli and there are a few different kinds of moduli that one gets. These moduli are massless if we don’t turn on the fluxes. That is a disaster because massless particles can actually cause extra forces to appear in nature which we don’t observe at all. Therefore, we need to make these moduli massive. The procedure to do that is called ‘moduli stabilization’.
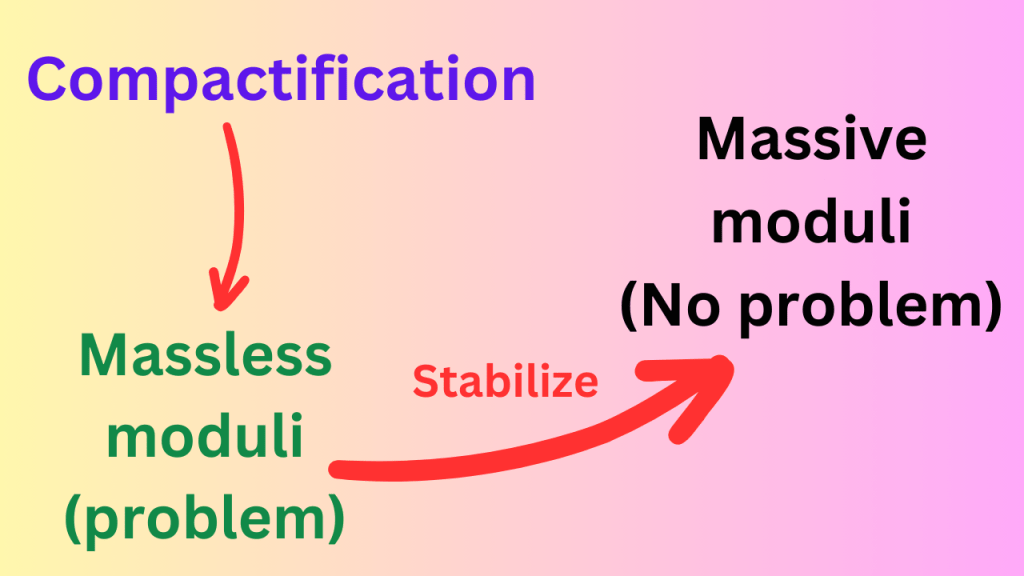
There are many approaches to stabilize the moduli. At the end of the day, we just want to generate a potential energy function (with a minimum point) for the moduli fields. This will make the moduli massive. One approach is to turn on the fluxes. It turns out that for type IIA theory, we can make all moduli massive just by using fluxes. However, in type IIB, there is no way to do so by just using fluxes. For type IIB, additional techniques are used e.g. including non-perturbative effects to stabilize the moduli.

In this article, we have only talked about getting dS from type II theories. We can try to get dS spacetime from heterotic strings as well. There are some physicists who think that we can’t get dS from string theory and the real vaccum is AdS while the dS spacetime is not the true vaccum. To read more about the view that we may not get dS from string theory (and how it may not be a bad thing), see this paper by Danielsson and Van Riet.
To read more about string compactifications, read this review by Grana or this review by Kachru and Doughlas. Also, see this review for recent trends.
