This is a small post to argue that (-+++) metric is objectively better than the (+ – – -) metric. Before starting, let me mention that I studied QFT in the (+ – – -) metric (from Peskin and Schroeder) and I am still more used to (+ – – -) conventions for some calculations. Still, I think that (-+++) is objectively better.
Positive volume
In the (-+++) metric, the volume of a spatial slice is positive. This makes total sense because the volume of a spatial slice should be positive. A negative volume of space is unphysical. Moreover, if space has negative volume, then the volume of a larger spatial region will be a negative number with larger absolute value. In contrast, the volume of a smaller spatial region will be a negative number with smaller absolute value. However, we know that negative numbers with larger absolute value are actually smaller than the negative numbers with smaller absolute value. Therefore, the (+ – – -) convention assosiates a larger spatial region with a smaller volume. This is a disaster.
Positive length
Consider two points in a spatial slice. In the (+ – – -) convention, the smallest distance between these two points (i.e. the length of the smallest geodesic between these two points) will be negative. This introduces a problem for lengths which is similar to the problem for volumes discussed above. In addition to this problem, the spatial slice will not be a metric space anymore (a metric space requires the distance between two points to be non-negative).
Negative sign
An argument given for the “superiority” of (+ – – -) convention is the fact that momentum squared equals mass squared for this convention. In the (-+++) convention, there is an additional minus sign.
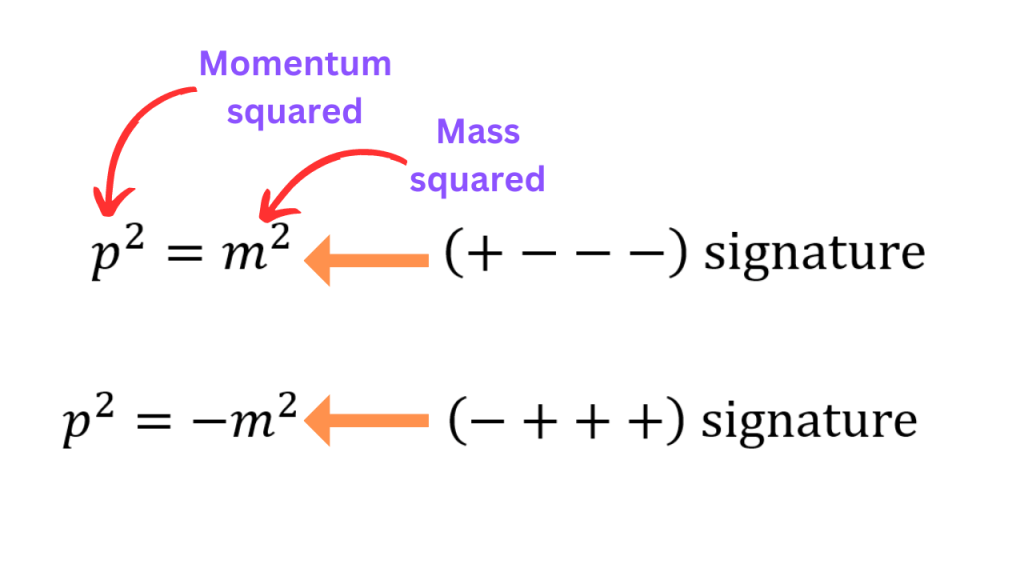
The (+ – – -) convention gives a nice looking relation, specially when one writes down the propagator of a scalar field (because it easily shows the location of poles in the momentum space).

The question that I want to raise is, “Why momentum?”. One can also talk about the second partial derivative. In the (+ – – -) convention, the Klein Gordon equation looks like the equation for momentum squared in (-+++) convention and vice versa.
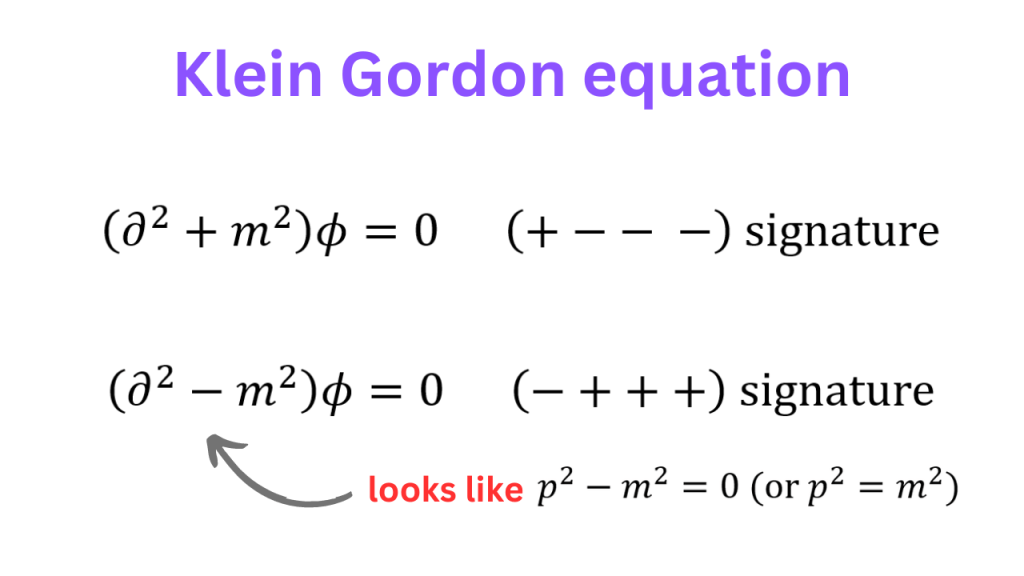
So, the insistence for momentum squared to be equal to a particular thing seems an arbitrary criterion to choose a convention for the metric signature.
Determinant of the metric
Higher dimensional spacetimes give a very good argument to choose (-+++) over (+ – – -). When we need to consider higher dimensional spacetimes (by adding more space directions), the (-+++…) convention will always keep the determinant of the metric negative (just like the four dimensional spacetime). However, the (+ – – -…) convention will change the sign of the determinant of the metric for every additional space dimension (it will be -1 to the power to space dimensions).

This extra factor would have to be included while writing the action, which is cumbersome. Moreover, the calculations where one needs to simultaneously deal with spacetimes of different dimensionality (e.g. string compactifications) keeping track of these extra factors for each spacetime is a nightmare.
These are some of the reasons why (-+++) is objectively better than (+ – – -). I rest my case.
