Hassaan Saleem

In this small post, I will show why the first few possible corrections to the Einstein-Hilbert action are the way they are. Basic familiarity with General Relativity is assumed.

I will use the natural units (units used in high energy physics) in this article. In these units, the unit of length is the inverse of the unit of energy (i.e. [Length]=[Energy]^-1). If you aren’t familiar with natural units, just take this fact on face value and you won’t be needing any more familiarity with them for this article.

Action is a quantity that is dimensless and it is a Lorentz scalar (i.e. it doesn’t change under Lorentz transformations). Action for a field theory is an integral of a Lagrangian density over spacetime. A generic term in the lagrangian density consists of a constant (called the coupling constant) multiplied by a quantity (called the operator). Since the volume measure of the 4-dimensional spacetime has dimension of [Length]⁴ (which is [Energy]^-4) the terms that appear in the Lagrangian density should have dimensions of [Energy]⁴ to make the action dimensionless. If the spacetime is curved, an additional factor of square root of the negative of the determinant of the metric appears in the volume measure. This determinant is dimensionless.

To make the Einstein Hilbert action (the action that describes pure gravity), we need some scalar made out of the quantities that describe the curvature. One such scalar is the Ricci scalar. However, Ricci scalar is made out of terms that have a double derivatuve or a product of two derivatives. These terms have a dimension of [Length]^-2 which is [Energy]² and thus, the required dimension of [Energy]⁴ isn’t acheived by Ricci scalar alone. In order to achieve this dimension, we divide the Ricci scalar by a quantity that has dimensions of [Energy]^-2. This quantity is nothing but the Newton’s constant G. So, the Einstein Hilbert action is shown in the diagram below.

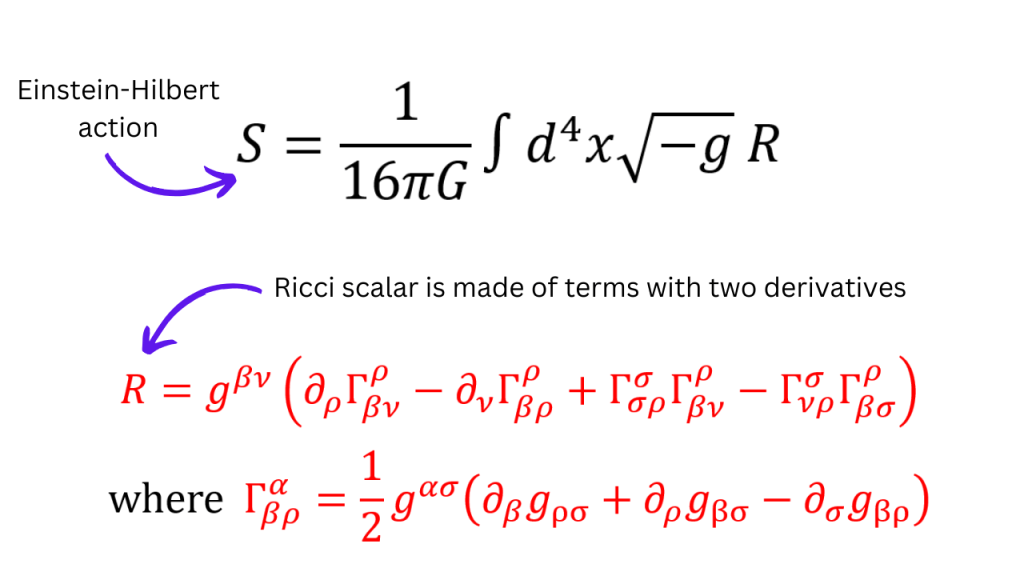
We saw that we acheived the required dimension of [Energy]⁴ by a combination of an operator i.e. the Ricci tensor and a coupling constant (i.e. G^-1). We could have started at a more elementary level by taking the operator simply as 1 (which is dimensionless) and a coupling constant whose dimension is [Energy]⁴ . This coupling constant is nothing but the cosmological constant. The Einstein Hilbert action with a cosmologival constant is shown in the picture below.

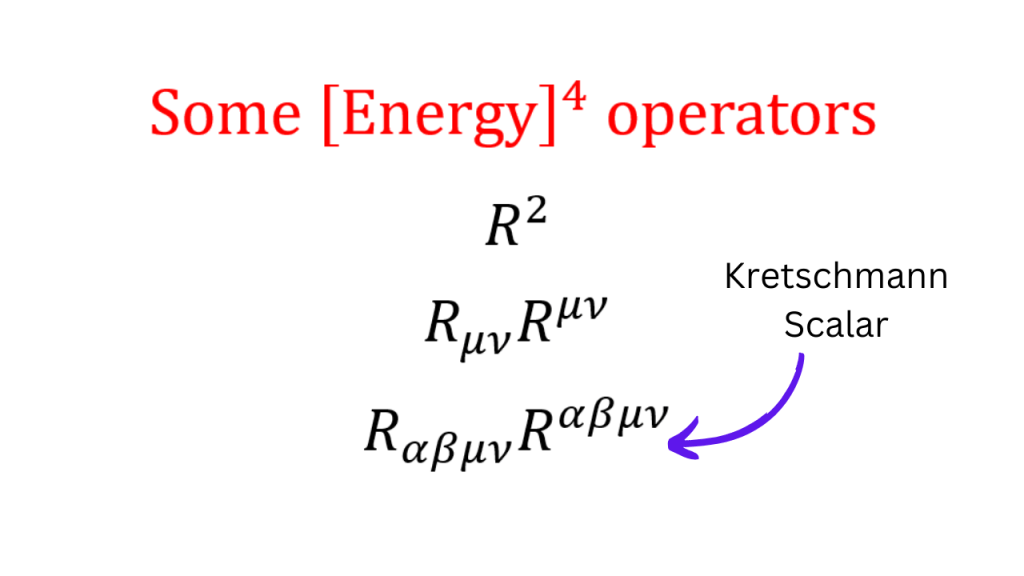
Now, if we want to add corrections to this action, the next logical step is to include terms with operators of dimension [Energy]⁴ which means that the coupling constants will be dimensionless. We saw before that the Ricci scalar has a dimension of [Energy]² and this is true for Riemann tensor and Ricci tensor as well (because these quantities too have terms with either a double derivative or a product of two derivatives).

Now, we need to figure out the operators made out of the Riemann tensor that have dimension [Energy]⁴. To do this, we can multiply Ricci scalar with itself, Ricci tensor with itself (with all indices contracted, so that the resulting operator is a Lorentz scalar) or Riemann tensor with itself (with all indices contracted). This last operator is called the Kretschmann scalar.

One may think that these are the only combinations that one can make but actually, there are some more combinations that we can make. Recall that the Riemann tensor is antisymmetric in its first two indices and it is also antisymmetric in its last two indices. Therefore, we can contract either the first two indices (or the last two indices) with the Levi Civita tensor and this gives us two different duals of the Riemann tensor called the left dual and right dual respectively. We can also contract the first two indices with the Levi Civita tensor, and the last two indices with another Levi Civita tensor at the same time and this gives us the double dual of the Riemann tensor.

These three duals opens up a lot of possibilities for us as we can contract these duals with each other and also with the Riemann tensor. However, it turns out that only two such possibilities are independent (all the other possiblities can be written in terms of these two independent quantities and the Kretschmann scalar). These two independent quantities are called the Chern-Pontryagin scalar and the Euler scalar.

Can these additional quantities be added as corrections to the Einstein-Hilbert action? The answer is no. This is so because if you compute the spacetime integral of either of these quantites, the resulting integrals are topological. It means that these integrals will not change if we do some continuous deformation (for example, if we deform the metric tensor). Recall that the Einstein equation is derived from the Einstein-Hilbert action by varying the action with respect to the inverse metric tensor. It means that these topological integrals won’t contribute any correction to the Einstein equation. Therefore, we don’t consider these terms for the corrections to the Einstein-Hilbert action.

As a side question, we ask that what properties of the spacetime do these topological terms compute? It turns out that the integral of the Euler scalar computes the “Euler characterisitic” of the spacetime (which is a well known topological invariant). The integral of the Chern-Pontryagin scalar is called the “instanton number” of the manifold. A reader familiar with the Yang Mills instanton will see parallels between this instanton number and the Yang Mills instanton number.

So, we are back to where we were before introducing the duals of the Riemann tensor. The three possible terms of dimension [Energy]⁴ are the square of Ricci scalar, square of (and contracted) Ricci tensor and square of (and contracted) Riemann tensor. However, the role of the Euler characteristic isn’t over yet. We can write down the Euler characteristic in an interesting form. This form is as follows.

So we see that we can write the integral of the Riemann tensor squared as a linear combination of integrals of Ricci scalar squared, Ricci tensor squared, and a topological term. But we discard the topological terms as discussed before. Therefore, we can eliminate all the Riemann tensor squared terms from the Lagrangian density and thus, the only terms of dimension [Energy]⁴ in the lagrangian density are shown in the picture below.