Hassaan Saleem

In this post, we will go through the reasoning that gives us the Schwarzchild solution of Einstein field equations. Prerequisites for this post include familiarity with Einstein field equations.

We start with the Einstein field equation (EFE) and convert it to a form that is used to solve this equation. This form is called the trace reversed form and to derive it, we contract EFE with the metric tensor.

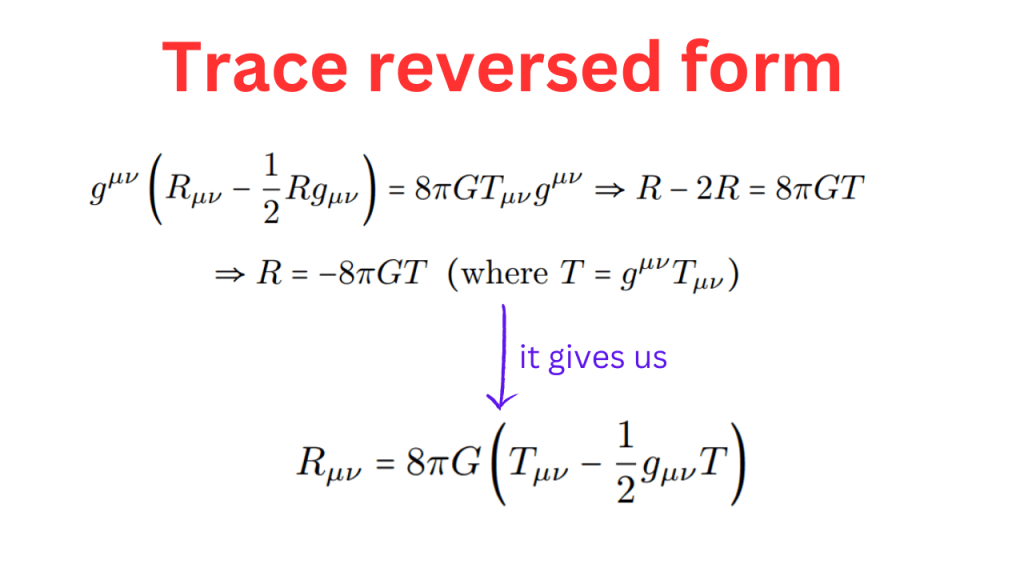
Now, we specialize to the case of the Schwarzchild metric which is the metric of an eternal, electrically neutral, and non-rotating black hole of mass M. This means that the metric tensor will be independent of time, and it will be spherically symmetric. This means that outside the black hole, the stress tensor is zero. Setting stress tensor equal to zero will also set T = 0 and thus the trace reversed form tells us that the Ricci tensor is zero as well.

Now, since the metric is spherically symmetric, the metric tensor in the (t,r,θ,ϕ) coordinates (which we will also refer to as (x⁰,x¹,x²,x³)) should have the form shown in the picture below (I am taking ϕ as the azimuthal angle).

We have used the fact that the metric tensor is symmetric. Since the metric tensor is independent of time, no component depends on t. In addition, since the metric has rotational symmetry about the z axis (it is a consequence of the spherical symmetry), no component should depend on ϕ as well. This means that under the transformations t → -t and ϕ → -ϕ, the metric tensor should be invariant. In addition, due to spherical symmetry, the metric should be invariant under the transformation θ → -θ as well.

Under these three transformations, some of the components transform to negative of themselves and thus, we can set these compnonents to zero to keep the metric invariant under these transformations. The story is shown in the following picture.

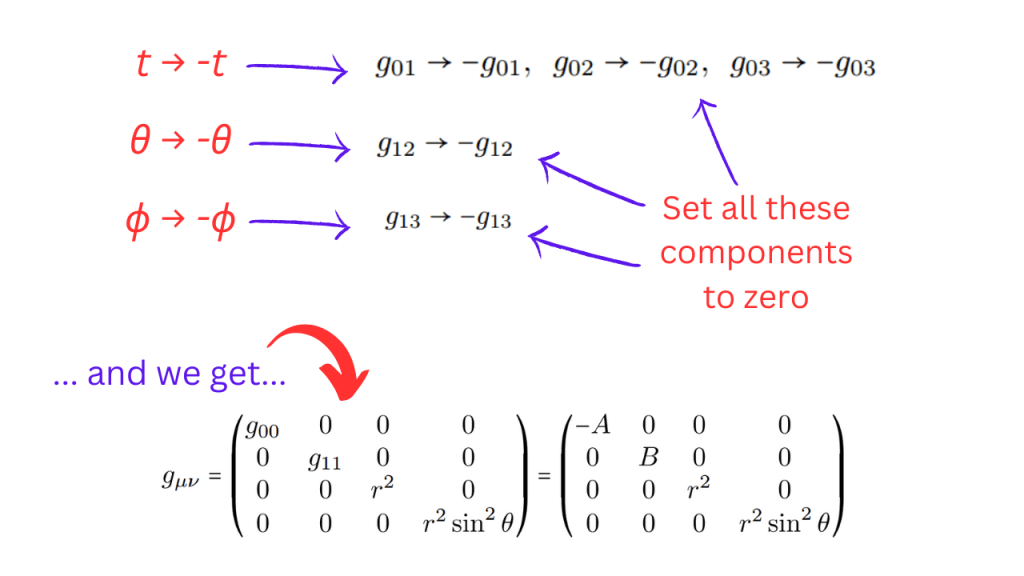
where we set g₀₀ = -A and g₁₁ = B. At a given value of θ and ϕ the metric tensor should be the same as any other value of θ and ϕ. At the given θ and ϕ, the metric tensor is composed of only A and B and thus, we see that A and B shouldn’t depend on θ but only on r.
Now, we use the expression for the Ricci tensor we calculate all the independent components (keeping in mind that Ricci tensor is symmetric and thus, we only need to calculate R₀₀, R₁₁,R₂₂,R₃₃, R₀₁, R₀₂, R₀₃, R₁₂, R₁₃ and R₂₃ only. We set these components to zero and the resulting equations are shown in the picture below (derivatives of A and B with respect to r are denoted as A′ and B′ respectively).

Let’s call the three boxed equations as (i), (ii) and (iii). If we add (i) and (ii), we get the conclusion that the product of A and B is a constant. If we put this result in (i), we will get some expressions for A and B. This process is shown in the picture below.

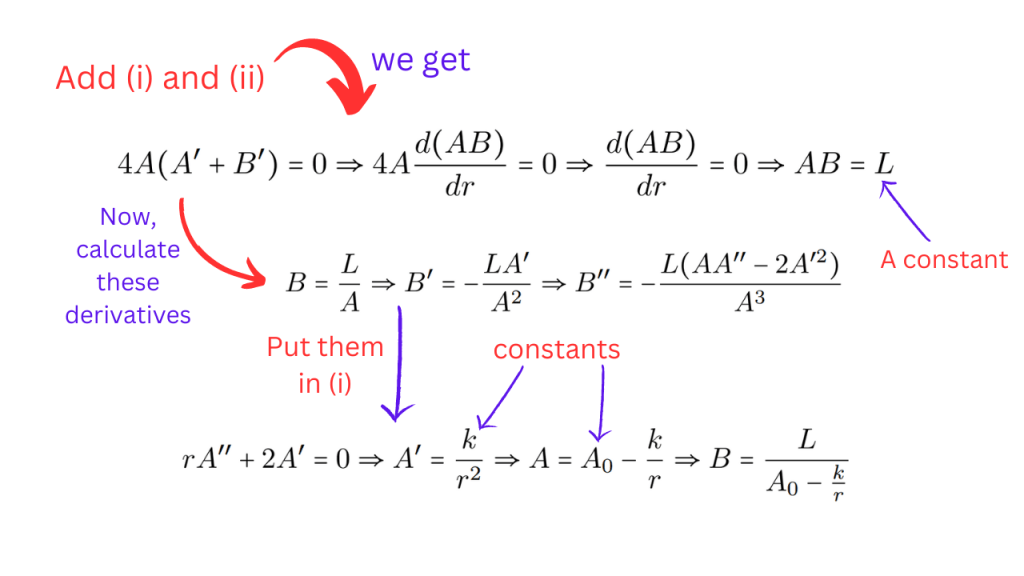
We can put these expressions of A and B in (iii) and that will set A₀=L. We can also determine L. We know that as r → ∞, the metric should approach the flat spacetime metric i.e. diag(-1, 1, 1, 1). Thus, A and B should approach 1 in this limit. We see that B does approach 1 but A approaches L. This means that L = 1.

We just need to determine k now. This is done by matching the predictions of this metric to Newtonian gravity in the weak gravity limit. But before doing that, observe that as r goes from r > k to r < k, the sign of g₀₀ and g₁₁ flip. This transition happens at r = k and thus, this radius is called the event horizon of the Schwarzchild black hole. Using these expressions the line element corresponding to the Schwarzchild metric is given in the following picture. Before going to the weak gravity limit, let’s restore the factors of c in the metric (where c is the speed of light). It will appear in the g₀₀ component.

Now, we use the geodesic equation with parameter τ. We consider the geodesic equation for the r coordinate and consider a motion in which θ and ϕ don’t change. We also set τ = t i.e. we take the coordinate time t as the parameter. Since the motion only happens in the r direction, we expect to recover something like Newton’s law. The proceedings are shown in the picture below.

We see that in the second term, we have dr/dt divided by c and we do know that dr/dt is radial velocity. We are working in Newtonian regime where speeds are much smaller than the speed of light and thus, we will drop any term proportional to velocity/(speed of light).

Secondly, we discussed before that k is the Schwarzchild radius of the black hole. For the Newtonian regime, we are considering motions are that are outside the black hole and happen at distances much bigger than the Schwarchild radius k. Therefore, k ≪ r and thus, we can expand the remaining term as a binomial expansion in k/r. We recover Newton’s law if we set k=2GM/c².

This is the requird value of k and thus, we have derived the Schwarzchild metric.