In this series of posts, I will explain what conformal field theories (CFTs) are. Basic familiarity with Quantum Field Theories (QFTs) is assumed.
In usual relativistic QFTs have some spacetime symmetries. These symmetries are rotations (one about every space direction), boosts (one along every space direction) and translations (one along every spacetime direction). The set of all rotations and boosts make the collectively make the Lorentz group and if we add translations to the mix, we have the Poincare group. Please note that boosts can be seen as rotations as well. These rotations mix a space direction with a time direction. Therefore in the future, when I write “rotations”, I mean rotations and boosts. We have generators for all the independent transformations in the Poincare group and their commutators form the Poincare algebra.

The defining feature of the transformations in Poincare group is that they keep the metric tensor invariant. We can change this by allowing the metric tensor to change by a factor (which is non-negative everywhere, because the metric tensor can’t be negative). Now, the transformations that allow such a change in the metric tensor are called conformal transformations.

If we consider arbitrary infinitesimal transformations, there is a simple equation that infinitesimal conformal transformations need to satisfy. From this equation, we can see that in 1 dimension, every transformation is conformal. We can also see that in arbitrary dimensions, conformal transformations are at most quadratic in x (there are some caveats to this statement that appear in two dimensions).

Since the conformal transformations are quadratic at most, one can deduce that the independent conformal transformations consist of translations, rotations, scale transformations (i.e. stretching and contracting spacetime) and a special type of transformations called the special conformal transformations (SCTs). The group of these transformations is called the Conformal group.
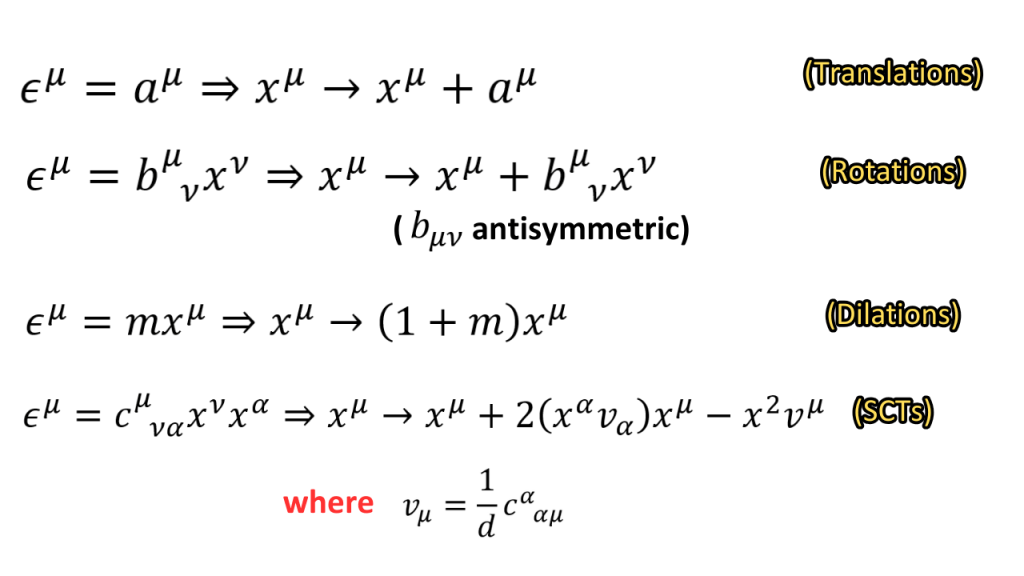
To make sense of SCTs, we consider the inversion transformation. An inversion send a position vector with length L to a position vector of length 1/L, without changing its direction. Now, SCTs can be seen as an inversion, followed by an arbitrary translation, followed by another inversion. Therefore, the only independence in choosing a particular SCT is in chooing the translation.

Therefore, we see that the conformal group contains the Poincare group. Just like the Poincare group, the generators of the Conformal group give us the conformal algebra (to be continued).

