This is the first post in a series of posts about the Swampland conjectures. In each post, I will discuss one Swampland conjecture. The basics of General Relativity and QFT are assumed for the readers of this series.
In this first post, we will discuss a conjecture called the “No global symmetries conjecture”. The statement of the conjecture simply states that “For a theory that couples to gravity, one can’t have a global symmetry”. This conjecture is concerned about fundamental global symmetries, and doesn’t forbid symmetries which are symmetries at low energies but don’t continue to be symmetries at high energies. Such symmetries are called accidental symmetries and canonical examples of these symmetries include baryon and lepton number in the Standard Model. Why do we think that this conjecture is true? There are multiple lines of reasoning to think so, and we will discuss them in the following.
Black Hole arguments
The most well known arguments come from black hole physics. Suppose that we do have a global symmetry in a quantum gravitational theory and we have some matter charged under this symmetry. Let’s throw this matter in the black hole. What happens then? We know that there is a well known theorem about black hole physics called the no hair theorem. This canonical statement of this theorem says that the only properties of a black hole that an outside observer can measure are its mass, electric charge and its angular momentum.
The reason why electrical charge can be measured from outside is that electric charge gives rise to a long range field (i.e. the electric field) which can be measured by an outside observer by measuring the flux of this field and using Gauss’ law. However, matter charged under a global symmetry doesn’t produce a long range field like the electric field, and thus, there is no way for an outside observer to measure the global charge of a black hole. This means that for a black hole with a given mass, there are multiple “versions” with each version having a different amount of global charge on it. Moreover, this global charge can be arbitrarily high as there is no reason to have a limit on this global charge. This implies that a black hole with a given mass would have infinite different versions and hence, an infinite entropy, which is in clear contradiction with Bekenstein-Hawking entropy formula.
We should recall that when it comes to electrically charged black holes, there is an upper bound on the amount of electrical charge that a black hole of a certain mass can have. This bound is shown in the image below. Therefore, the infinite entropy problem doesn’t arise for the electrical charge.

There are even more problems with global symmetries when we consider black hole evaporation. The immediate question that comes to mind is, “Can the black hole get rid of its global charge via hawking radiation?”. The answer to this question is “no” due to the following reasoning.
Black holes do get rid of its electrical charge via Hawking radiation and this radiation is generated at the horizon of the black hole. The generation of this radiation involves pair production and the falling of one of the particles inside the black hole. If the black hole is positively charged, the negatively charged particle falls inside the black hole and the positively charged particle escapes. This way, the black hole “gets rid” of its positive charge via the Hawking radiation. Now, one can ask that “How did the negatively charged particle know that it has to fall inside the black hole? Why didn’t the positively charged particle fall inside the black hole? What introduces this asymmetry between negatively and positively charged particles at the horizon?”. The answer is simple: The electrical field due to the charged black hole. Now, if a black hole has global charge only, this long range field is absent and thus, there is nothing at the horizon to introduce this asymmetry between positively and negatively charged particles. Therefore, the mechanism to get rid of the global chage via hawking radiation is absent.
So if the black hole can’t get rid of its global charge, what happens then? The charge can’t vanish in thin air of course because that will break unitarity (as we will lose the information about the global charge). One possibility is the presence of remnants. Remnants are speculative end-products of black hole evaporation. The phenomenon of black hole evaporation is deduced on the basis of semi classical physics (which means that we assume a classical spacetime and have quantum field on this spacetime) but when the evaporating black hole becomes very small (of the order of Planck scale), some additional quantum mechanical effects might take over and thus, the description of an evaporating black hole may not be the right description in this regime. One speculation is that the evaporation comes to a halt in this regime and gives rise to long lived objects called the remnants.
Since a black hole can’t get rid of its global charge, this charge can end up in the remnant. However, as we saw earlier, the global charge on a black hole can be arbitrarily high and thus, infinitely different versions of these remnants are possible (each with a different value of the global charge). An infinite number of different possible light particles destroys the low energy physics, and therefore, the presence of global symmetries in quantum gravity leads to the break down the low energy physics, which is in clear contradction to what we know about low energy physics in the presence of gravity.
Baby Universe reasoning
Another line of reasoning against the presence of global symmetries in quantum gravity comes from the possibility of baby universes. So what are baby universes? In quantum gravity, we have quantum mechanical fluctuations in the fabric of spacetime, and to calculate the gravitational path integral, we have to sum over all the possible fluctuations. This sum also involves summing over different topologies of spacetime. These topologies involve having spacetime with wormholes and geometries where a region is branched out of the main body of spacetime, with the branch pinching off, giving an extra component. This process is shown below
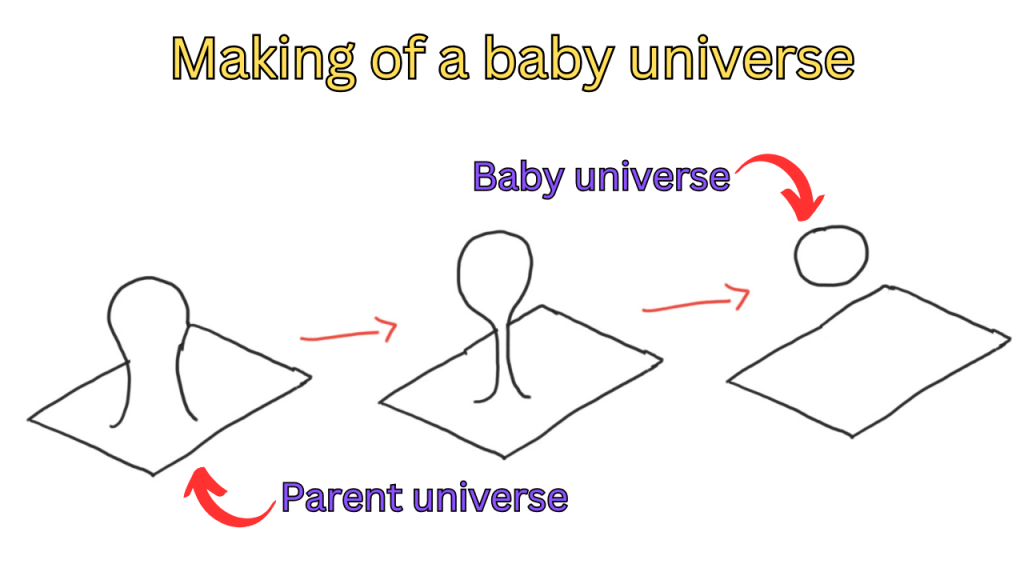
This extra component is called a baby universe and the main body of spacetime is called the parent universe. Now, “Can some charge that was present in the parent universe, disappear from the parent universe and go to the baby universe?”. Let’s see what would happen if we start with some electrical charge. If we try to do the branching and pinching process with the electrical charge in the baby universe, we immediately have a problem. Since the field lines lines can’t end abruptly, this process seems to be impossible, unless there is some induced charge in the parent and baby universe. So, the electric charge in the parent universe can’t just vanish and appear in the baby universe.
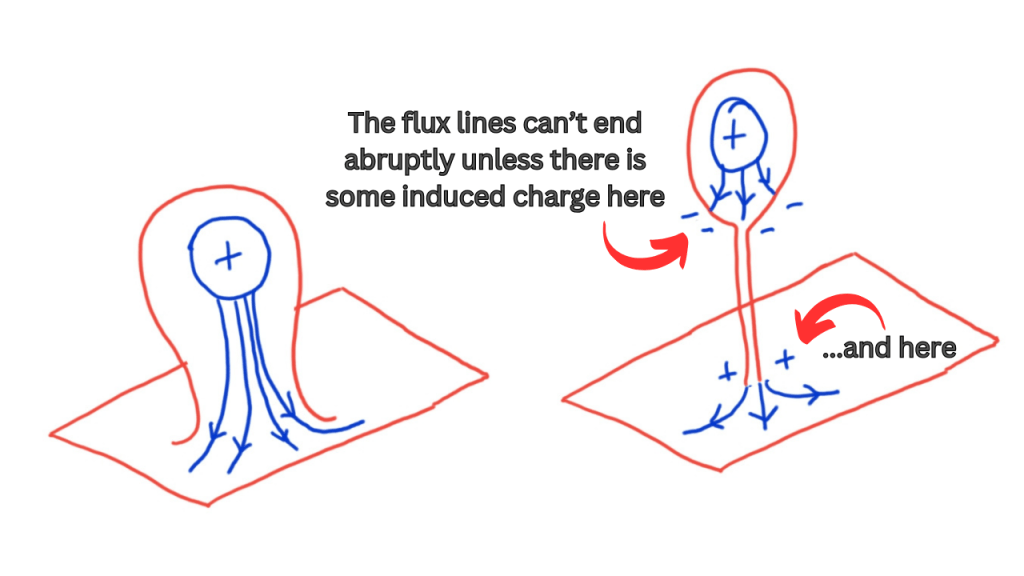
For the global charges, this deterrence isn’t there because the global charges don’t have a long range field, and thus, no field lines coming out of them. Therefore, global charges can easily vanish from the parent universe and appear in a baby universe. This means that the charge isn’t conserved for observers in the parent universe. One may say that if we consider both the parent and baby universe, the charge is still conserved, but that will happen only for some “super” observer that can access both universes somehow. As far as the observers in the parent universe are concerned, they can’t access the baby universe.
If we think in terms of the quantum states, the collective state of the parent and baby universe is a pure state but the observers in the parent universe have no idea about the state of the baby universe and they have to describe the state of their universe by a density matrix ( this would be done by tracing over the density matrix of the baby universe). It would imply that the quantum mechanical evolution of the parent universe is non-unitary, which is another undesirable feature.
Holography argument
The last line of reasoning comes from holography. Holography includes a gravitational theory on a spacetime (called the bulk) with a non gravitational theory on the boundary of this spacetime. The gravitational and non gravitational theories are dual to each other and every object/phenomenon in one theory has a dual object/phenomenon in the other theory.

Now, suppose that we have a global symmetry in the gravitational theory (on the bulk side). What does this global symmetry correspond to in the boundary theory? One may say that it can be a global symmetry in the boundary theory. However, that can’t be the case because it is well known in holography that any global symmetry in the boundary theory corresponds to a gauge symmetry (and not a global symmetry) in the bulk theory. There is a simple way to see this. The global charge for the global symmetry in the boundary theory is conserved and thus, whatever this global charge corresponds to on the bulk side should be conserved as well. A while ago, we saw that in gravitational theories, global charge isn’t conserved (due to possible baby universes) and thus, the global charge in the boundary theory can’t correspond to some global charge in the bulk theory. Gauge charges on the other hand, would be conserved in the bulk theory (because they don’t vanish into baby universes) and are natural candidates for the dual of global charges in the boundary theory.
Therefore, there is no viable candidate for the dual of global symmetry in the bulk. One can’t have global symmetries in the bulk without having some dual on the boundary side because that will destroy the duality. The natural way out of this dilemma is that there are no global symmetries on the bulk side (i.e. in the gravitational theory).
