Hassaan Saleem

To make a theory that has bosons and fermions in it, we start with an action that has some free bosons which have two parts called the left moving part and the right moving part. We have D such bosons in total where D is the number of spacetime dimensions. We also have D right-moving fermions and D left-moving fermions.

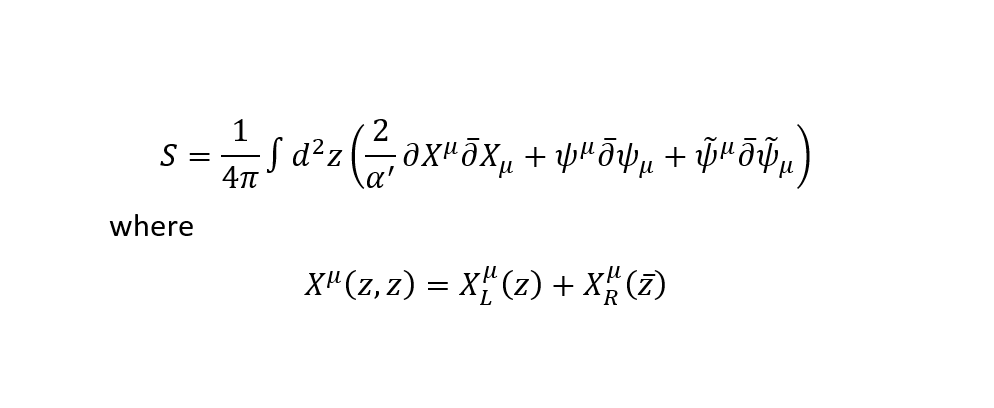
Now, if the theory is defined on a cylinder (because a closed string can trace out a cylinder while moving in spacetime), then the bosonic fields don’t change when we go around the cylinder once but the fermionic fields can acquire a negative sign.

If the fermionic fields do acquire a minus sign, we say the theory is in Neveu-Schwarz (NS) sector and if they don’t acquire a minus sign, then the theory is said to be in the Ramond (R) sector. Since we have left and right fermions, we can have (NS, NS), (NS, R), (R, NS) and (R, R) sectors where the first label is for the left fermions and the second label is for the right fermions.

However, it turns out that these labels are not enough. We also need to count the number of fermionic operators required to make a state. We measure it by worldsheet fermion number F. It is even if the number of fermion operators is even and vice versa. So (-1)^F if +1 is F is even and -1 for odd F.

So, we can have NS+, NS-, R+, and R- sectors (where + and – denoted the value of (-1)^F). For closed strings, we can have all possible combinations of these e.g. (NS+, NS+), (R+, R-), (R+, NS+), (R-, R-), etc. Now, only the NS sector has a tachyon in it and because of a consistency condition called the level matching condition, NS- the sector can only come with itself. So, (NS-, NS-) is the only sector where NS- appears.

So, the possible sectors are (NS+,NS+), (NS+,R+), (NS+,R-), (R+,R+), (R+,R-),(R-R-). I have not included (R+,NS+) and (R-,NS+) again because they give the same kind of excitations of the string as (NS+,R+) and (NS+,R-).

The question now arises that what kind of sectors are actually allowed? Are all of them allowed? To constrain the possibilities, we use three very reasonable conditions on our theory that I will describe below.

The first condition is called mutual locality. It simply means that if there are two operators (called the vertex operators in the string theory context) from two sectors, then if we rotate one operator a full circle around the other operator, the operator should be invariant. To be more precise, when one operator rotates around another one in our formalism, it can at most get multiplied with a phase. So, we require that this phase is one.

The second condition roughly says that if we multiply two operators from any two allowed sectors in a theory, then all parts of the result of that multiplication should also be operators in that theory. Technically, we say that the operator product expansions close.

The last condition is a consistency condition called modular invariance. It is hard to describe here but it is necessary to have consistent string theories on different two-dimensional surfaces. This requirement implies (after a long argument) that we must have at least one left and right R sector.

We can solve it for two cases. We either have at least one (R-,NS+) or (R+,NS+) sector or we have none of them. If we have at least one of them, we have four possible sets of sectors (i.e. four possible theories) as solutions which are as follows

1- (NS+,NS+),(R+,NS+),(NS+,R+),(R+,R+)

2- (NS+,NS+),(R+,NS+),(NS+,R-),(R+,R-)

3- (NS+,NS+),(R-,NS+),(NS+,R+),(R-,R+)

4- (NS+,NS+),(R-,NS+),(NS+,R-),(R-,R-)

The first and last are related if we do a spacetime reflection in any one direction. The second and third are also related to each other in the same way. So, there are two possible solutions at the end.

IIA: (NS+,NS+),(R+,NS+),(NS+,R-),(R+,R-)

IIB: (NS+,NS+),(R+,NS+),(NS+,R+),(R+,R+)

As labeled appropriately, these are the Type IIA and Type IIB theories. Even these theories are related to each other if the theory is compactified in some dimensions. If we do a transformation called T transformation in one direction, type IIA becomes type IIB and vice versa.

Note that in type II B, all (-1)^F=+1. So, (-1)^F is always +1 in both the left & right sectors in type II B. In type II A, the left sectors always have +1 but the right sector has (-1)^F=-1 when the R sector appears. These selection rules are called the GSO projection.

We can also solve the case when there are no (R-,NS+) or (R+,NS+) sectors. This gives us type 0 theories but they always have tachyons because they have (NS-,NS-) sector. Note that the type II theories don’t have (NS-,NS-) sector and thus, no tachyon.