Hassaan Saleem

This is first in a series of posts on duality between strings moving on AdS₃ x S₃ x T₄ spacetime (don’t get intimidated by this) and a conformal field theory living on the boundary of the AdS₃ spacetime (which is two dimensional). I will try to explain the basics required to understand this duality. In this first post, I will briefly describe what AdS₃ spacetime is. For this post, I assume basics of general relativity.

The fact that characterizes all AdS spacetimes is that they have constant negative curvature. Let’s define AdS_n spacetime. It is a spacetime with n-1 dimensions of space and 1 dimension of time. To see how this spacetime looks like, we need to understand some spaces called hyperboloids.

Let’s start with the equation of a two dimensional sphere with radius R. It is given as follows

What will happen if I switch some of the plus signs on the left hand side above into a minus sign? The sphere turns into a hyperboloid. We can turn either one or two plus sign to a minus sign. This gives us two different hyperboloids which are shown as follows.

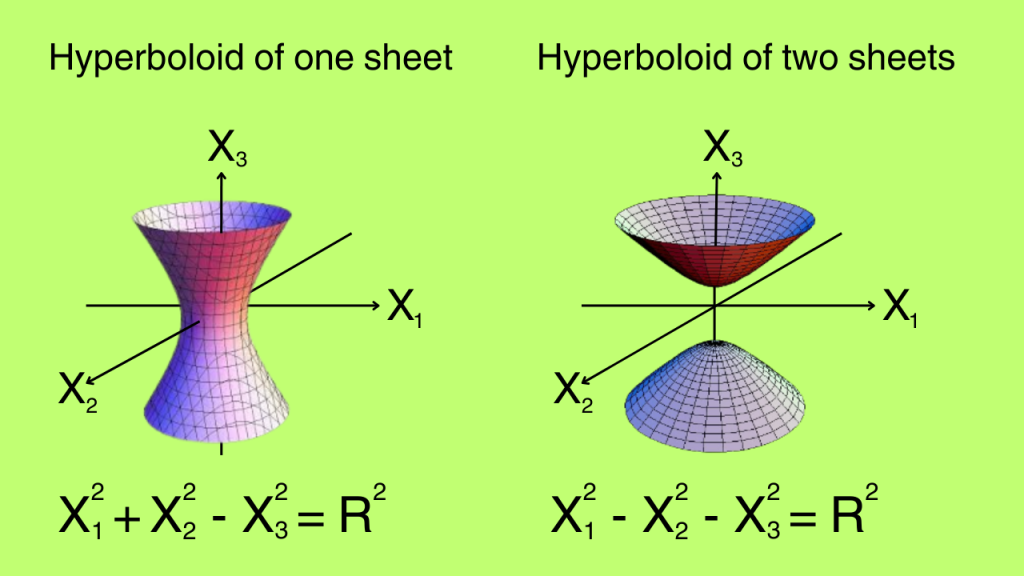
Now, if we take the equation for the hyperboloid of two sheets and change the sign of the term on right hand side, we get the AdS₂ spacetime.

Note that the equation of the two dimensional hyperboloid was written in a space of one higher space dimension. In contrast, the equation of the AdS₂ spacetime was written in a space of one additional time dimension.

We can generalize the equation above to write down the equation that describes AdS_n by using coordinates of an n+1 dimensional spacetime with n-1 space and 2 time dimensions (it is called a (2,n-1) spacetime).

So now we can see that the equation for AdS₃ is as follows.

If we want to describe AdS₃ with three coordinates, we can choose the following three coordinates that satisfy the equation of AdS₃ above. These coordinates are called the global coordinates. One can also derive the metric of AdS₃ in these coordinates.

In these coordinates, AdS₃ can be seen as the cylinder with the following coordinate assignments to different directions.

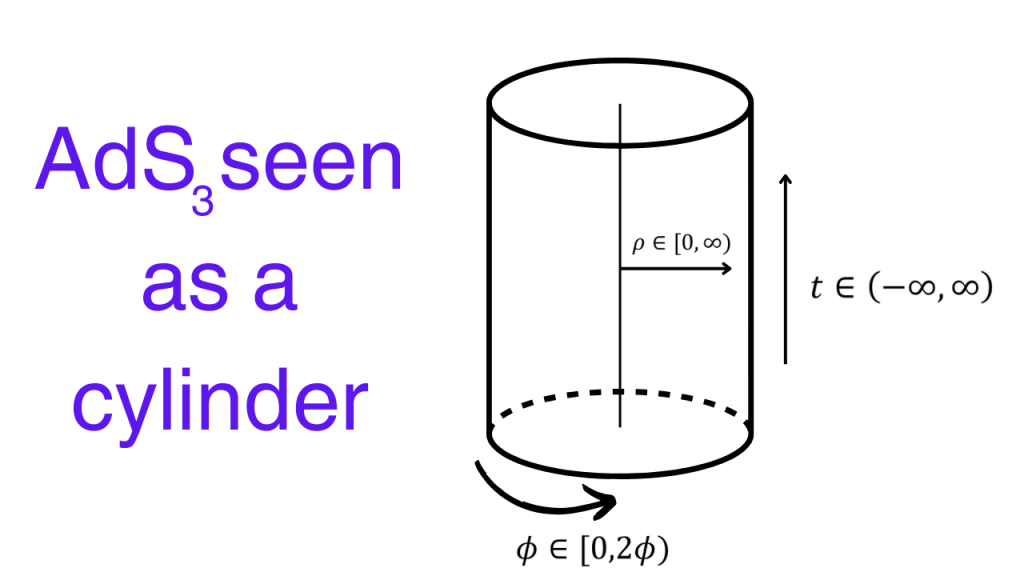
Note that ρ goes from zero to infinity instead of going from 0 to a finite radius (which is the case for normal cylinders).

Let me make a final remark. The group of 2 x 2 real matrices with determinant equal to 1 is called SL(2,R) (R here means real numbers). A general element of this group can be written as follows.

One can easily see that the equation satisfied by the parameters of SL(2,R) is the same as the equation describing AdS₃. However, it doesn’t mean that AdS₃ is the same as SL(2,R) and we will see that it turns out that SL(2,R) and AdS₃ have a major difference.

However, we can see that SL(2,R) has similarities with AdS₃ and it will turn out in a future post that SL(2,R) is extremely useful to study strings on AdS₃. (To be continued)