Hassaan Saleem

Following the recent results announced by DESI, the interest in quintessence models may increase dramatically. So, this is a good time to write a small post on the basic ideas behind quintessence. Basics of GR and QFT are assumed for this post.

Firstly, let’s review the basic idea of a cosmological constant. The Einstein equation without a cosmological constant is still a consistent equation. For example, the contraction of both sides with a covariant derivative vanishes (I will refer to this contraction as divergence from now on).

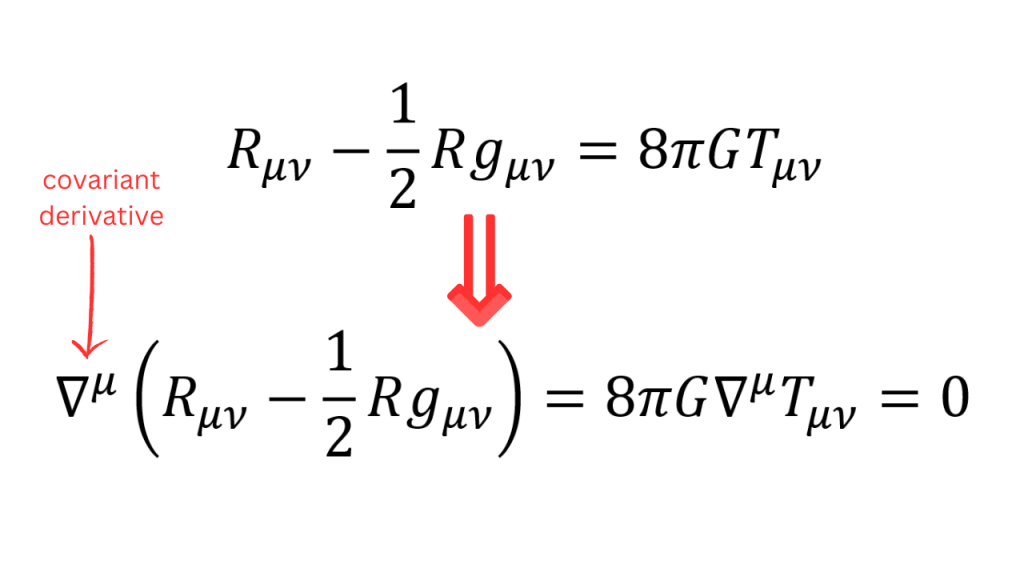
However, a nice property of the covariant derivative is that when it acts on the metric, it gives you zero. It means that on the left hand side of the Einstein equation (i.e. the geometry side) you can add a term proportional to the metric tensor and the divergence of both sides of the equation will still be zero. This is why the concept of a cosmological constant is even possible.

However, you can see that if Λ depends on the spacetime points i.e. if we have Λ(x) instead of Λ, then the divergence of this extra term won’t automatically be zero. Therefore, you can’t just add a spacetime dependent cosmological “constant” to Einstein’s equation.

Until now, I have only talked about general relaticity itself and I haven’t talked about cosmological considerations. From cosmological observations, we have learned that our universe is same in all directions at large distances (i.e. it is “isotropic”) and at any given time, every point in space (at large distances) is on the same footing (i.e. the universe is “homogenous”). These two properties can be stated more rigorously using the concept of Killing vectors of the metric tensor, but we don’t need to go down that road for our discussion.

Based on these observations, cosmologists have come up with a solution of the Einstein equation that is isotropic and homogenous. This solution is called FRW solution (also known as FLRW solution). This solution has two parameters called k and a. The parameter k can be 1,0 or -1 depending on whether the universe is closed (i.e. it has a positive curvature like a sphere), flat (has zero curvature, like a flat plane) or open (has negative curvture, like a Pringle chip or a saddle). In the case of our universe, we use the flat case i.e. k=0. The parameter a is positive, dependent on time and is known as the scale factor. It tells you the size of the universe at time t.

Einstein equations give us the equations of motion that a(t) needs to satisfy and they are called the Friedmann equations. These equations also include the pressure and volume of some other entities present in the universe. If there are more than one non interacting entities, there will a corresponding term for the pressure and energy density of each such entity in these equations. Dots represent time derivatives in the following picture.

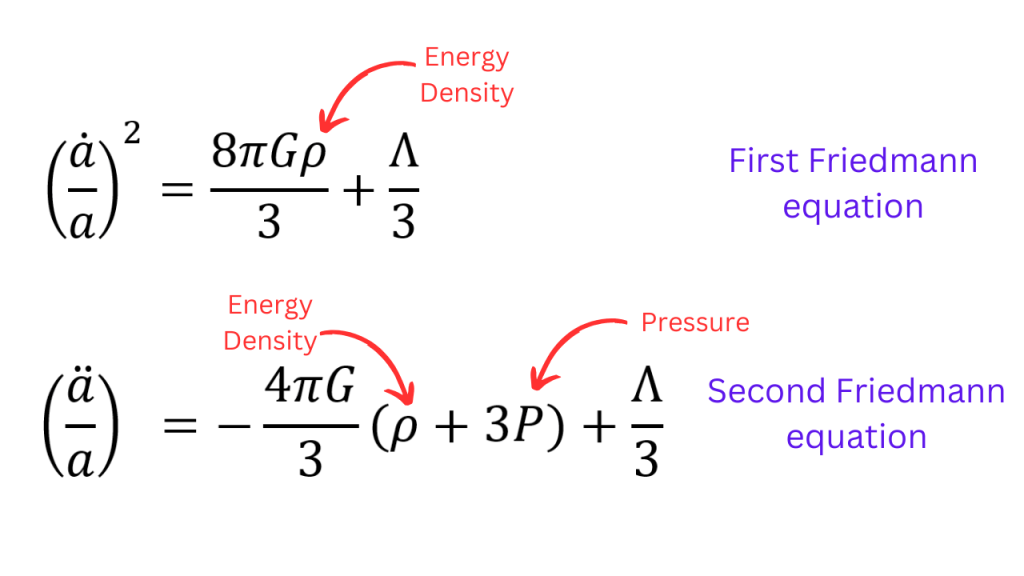
Now, for most kind of matter species that we study in GR, the energy and pressure follow an equation of state where the pressure is directly proportional to energy density, with the constant of proportionality called w. For the cosmological constant, w=-1, for photons, w=1/3, for dust, w=0 and for normal matter, w>0. If we use this equation of state, then the second Friedmann equation becomes the following

Now, the question is, how can we get something that acts like a time dependent cosmological constant. We saw earlier that having a time dependent cosmological constant itself won’t work. One hint comes from the second Friedmann equation. For a constant ρ, the term involving w can behave like the cosmological term, as both of these terms are just constant. To mimick a term with Λ>0, we need to make sure that 1+3w<0 which means that w<-1/3. Moreover, if we can find an entity for which w is time dependent, then we can get a term on the right hand side of the second Friedaman equation that behaves as if we had a time dependent cosmological constant. Note that we only want time dependence and not space dependence. If we get such an entity, we can just forget about the cosmological constant and set Λ=0.

But what entity is it? We saw earlier that for photons and dust, w is constant. So, it can’t be them. The answer is that we come up with a scalar field Φ called quintessence and this field does the job for us. Why a scalar field? Why not a vector field? Well, to conserve isotropy. If we use any field, we want that field to be constant at a given time. If we have any field other than a scalar field, having a constant configuration of that field at a given time with break isotropy (e.g. a constant vector field at a given time will pick a direction in space) unless that field is zero at all times, which gives a useless theory.

Does a scalar field give us a time dependent w? To see that, we need to calculate its pressure and energy density. To do that, we need to caclulate the stress tensor for Φ (assuming only time dependence for Φ). The lagrangian of Φ can contain a potential function V(Φ) and we have different quintessence models based on what V(Φ) is. The procedure to calculate the stress tensor is given in the following picture (remember that we are using the (-+++) signature, as everyone should)

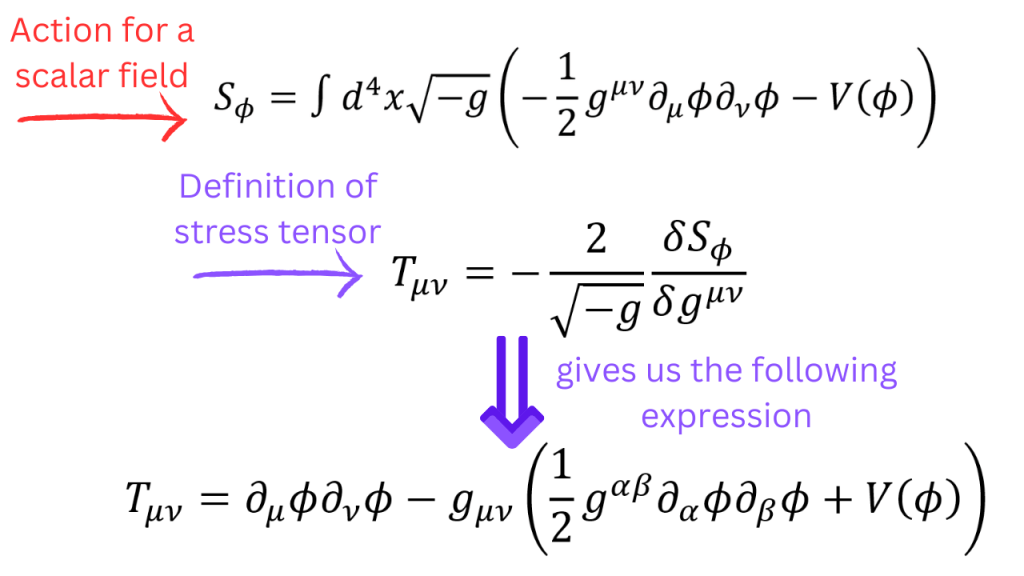
Now, the energy density of Φ is just the (0,0) component of the stress tensor but the pressure component in the i-th space direction isn’t the (i,i) component. It is actually the (i,i) component with the first component raised. This is because of the definiton of what pressure is. Pressure at a point is what an observer in a local inertial frame at that point measures (for whom, the metric around that point is the flat Minkowski metric). This gives us the following expression for w and we can see that it is definitely time dependent.

Recall that we estsablished earlier that for an entity to mimic a positive time dependent cosmological constant, w<-1/3. Imposing this condition tells us that the potential V(Φ) should dominate the square of the time derivative of Φ. It means that V(Φ) is positive. Also, notice that the smallest value of w that can take place is when the numerator in the expression of w is as negative as possible, which happens when Φ is time independent. In this case, w=-1, just like the cosmological constant. Therefore, for a quintessence field, w is between -1 and -1/3.